President’s Message – Fall 2022

AIHPresident Jamil IbrahimThis is an overdue update to our AIH members and community about what your AIH leadership team has been up to this year. I am thrilled to announce completion of critical and timely updates to the governing documents for our organization – our AIH Articles of Incorporation (formerly, Constitution) and AIH Bylaws. We initiated the review and update process in 2016. Over the past six years, past and current AIH leadership team members devoted many, many hours to completing a comprehensive review and developing suggested revisions to these documents. This review and update provided a great opportunity to reflect on how we have operated and how we will function in the future. In the spirit of these changes, Leonardo Da Vinci once remarked (translated to English): “When you put your hand in a flowing stream, you touch the last that has gone before and the first of what is still to come.” It is extremely gratifying to see the results of our review/update process in our new governing documents, and I look forward to the next steps.

There are many other great updates to share:

·        Diversity, Equity, and Inclusion (DEI) Committee – Our DEI Committee developed and prioritized a list of initiatives and solicited feedback/input on implementation through a virtual meeting held in March of 2022. Please reach out to Julé Rizzardo (President-Elect) to join the DEI Committee and learn about these great initiatives.

·        Annual Meeting – Our leadership team held our (delayed) Annual Meeting virtually during March 2022. The meeting was supposed to be held during December 2021, to set our trajectory for 2022, but was delayed due to COVD concerns. In addition to specific tactics associated with strategies and goals that were identified by the Executive Director and members of our Board of Directors, we established three “working groups” to address: (1) Technical Journal/Conference Collaboration; (2) promotions, swag, and marketing; and (3) coordination with affiliate organizations. Contact myself or our management office to learn more and get involved. We are scheduled to get back on track and hold our Annual Meeting in December of 2022 (hopefully, in-person) and set plans for 2023.

·        AIH Webinars – Continued our AIH webinars with great presentations by AIH members Richard Koehler (PhD, PH) and Andrew Cohen( PhD, PH).

·        Engagement with Affiliate Organizations – Continued our engagement with other organizations through promoting PH certification for hydrologists and HT certification for hydrologic technicians at the 2022 World Environmental & Water Resources Congress (EWRI); Frontiers in Hydrology Meeting co-sponsored by the American Geophysical Union (AGU) and CUAHSI (Consortium of Universities for the Advancement of Hydrologic Science, Inc.); and 11th International Symposium on Managed Aquifer Recharge (ISMAR).

·        AIH 2022 Awards – We Issued our distinguished AIH awards to our 2022 award winners: Bruce Wilson, PhD (Ray K. Linsley Award for Surface Water); Todd Halihan, PhD (Charles V. Theis Award for Groundwater); and Vijay P. Singh, PhD, PH (Robert G. Wetzel Award for Water Quality). Note, we will present these awards to our award winners this year at the American Water Resources Association (AWRA) 2022 Annual Conference during their Awards Luncheon on November 9, 2022, in Seattle, Washington.

·        Examination Questions Database Update – We have a plan in place and are about to embark on a comprehensive update to our database of examination questions for our AIH certification exams. Updates will be completed prior to our next round of examinations, scheduled for November 2022.

As I’ve stated in each of my messages previously, member participation is vital to AIH’s success. We are eager to engage more members in AIH activities. Please reach out to our Secretary/Membership Liaison, Jolyne Lea, at membership@aihydrology.org, to get involved.

Sincerely,

Jamil S. Ibrahim PH, PMP, ENV SP
AIH President, 2021-2022

Spotlight on Recent AIH Exams and on New Members

Congratulations to those who recently passed their exams during May 2022!

Hydrologist-in-Training – Fundamentals (Part I)

Madeline Richards, HIT

Kaiylyn Chow, HIT

Robert Sheridan, HIT

Professional Hydrologist – Principles and Practices (Part II)

John Shuler, PH (Surface Water)

Benjamin Von-Thaden, PH (Surface Water)

Congratulations to New Members

Congratulations to those who have been recently certified as Professional members of the American Institute of Hydrology!

Max Strickler, PH (Surface Water)

Matt Sparacino,  PH (Surface Water)

John Shuler, PH (Surface Water)

Benjamin Von-Thaden, PH (Surface Water)

Recap of AIH Webinars

AIH was honored to feature two webinars by outstanding hydrologists and AIH members, Richard Koehler, PhD, PH, and Andrew Cohen, PhD, PH.

On June 16th, Dr. Richard Koehler presented a webinar titled, “A Novel Approach to Quantify Streamflow Properties”. During the webinar, Dr. Koehler presented a novel approach using autocorrelation lag (k) plots and sequence summations to quantify several stream flow properties, including magnitude, frequency, duration, timing, and rate of change. To learn more about the approach, please refer to his article featured in this Bulletin titled, “The Lag 1 Hydrograph – Alternate Way to Plot Streamflow Time-Series Data”.

In collaboration with the American Water Resources Association (AWRA), AIH presented a webinar on July 13th by Dr. Andrew Cohen titled, “Introduction to the GroundwaterU Video Public Library – a new and free educational resource”. During the webinar, Dr. Cohen introduced GroundwaterU as an educational platform that serves to make groundwater knowledge accessible globally by way of high-quality and engaging educational videos. For more information about GroundwaterU, please visit the following link: Home – GroundwaterU

Institute Development Recap

AIH continues to collaborate with other professional organizations in order to promote our common goals of enhancing and strengthening the standing of hydrology as a science and profession. Through other organizations, we have been reaching out to hydrologists, hydrologic technicians, and students currently pursuing formal education in a field related to hydrology.

On April 12 -14, 2022, AIH collaborated with Groundwater Resources Association’s (GRA’s) 11th International Symposium on Managed Aquifer Recharge (ISMAR11), held in Long Beach, California, by contributing financially to their World Access Sponsorship. This sponsorship helped provide free live-streaming access to attendees joining virtually from other countries who were not able to travel to the conference.

On June 6-8, 2022, AIH Board of Directors members, Yige Gao, PH (Director, International Affairs) and George McMahon, PhD, PH (Director, Policy and Advocacy) attended the American Society of Civil Engineers (ASCE) Environmental and Water Resources Institute (EWRI) Congress in Atlanta, GA, where they presented and initiated partnerships with other hydrology-related organizations. Yige also presented on ‘Certifying the Practice of Hydrology’ for a student session.

On June 19-24, 2022, AIH Board of Directors member, Zhong Zhang, PhD, PH (Director, Academic Affairs) attended the Frontiers in Hydrology Meeting (FIHM), Puerto Rico, which was co-sponsored by the American Geophysical Union (AGU) and Consortium of Universities for the Advancement of Hydrologic Science, Inc. (CUAHSI). AIH purchased a meter board to reach out to hydrologists and promote our membership. Zhong interacted with conference attendees interested in learning about AIH and its membership.

Photo: Dr. Zhong Zhang standing next to the AIH meter board, at the June CUAHSI-AGI Conference, Puerto Rico.

The Lag-1 Hydrograph – An Alternate Way to Plot Streamflow Time-Series Data

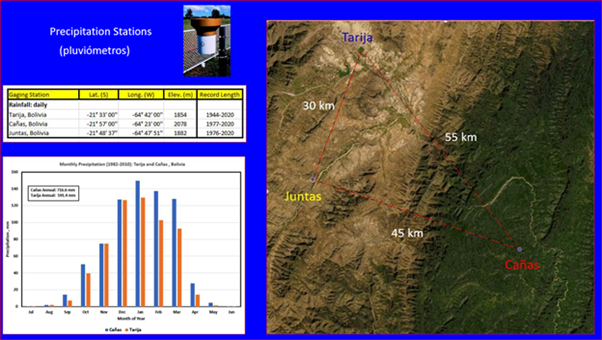
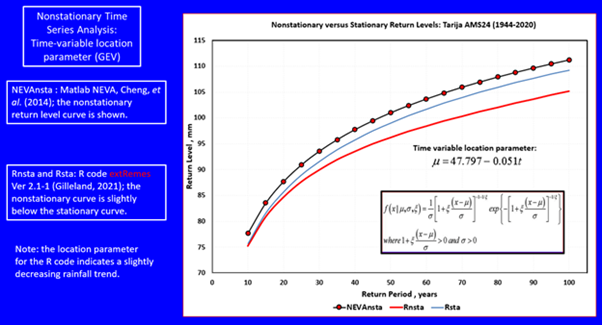
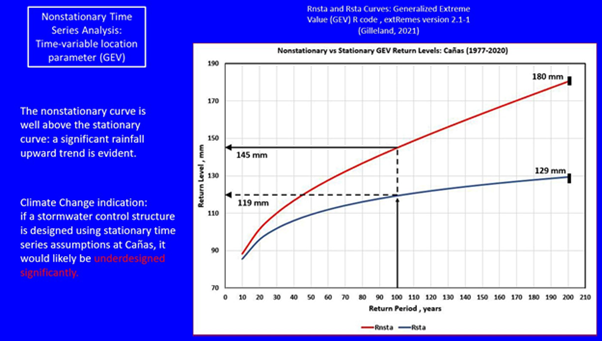
Abstract

An alternate approach is presented where graphing discharge can be accomplished without a time axis. This technique allows data properties such as Q, dQ/dt, and d2Q/dt2, and trends of increasing, decreasing or no change flow to be readily seen and understood on a single graph. Flow pulse reference lines can easily be added and interpreted. The methodology is based on the time-series serial correlation lag-1 graph and uses the normally unwanted (but still valuable) autocorrelation present within the streamflow data. Examples and applications are included.

Key words: Lag-1 hydrograph, autocorrelation, 1st, 2nd order derivative, hydrograph analysis

Introduction

Hydrographs are an essential tool for hydrologists or other water resources professionals. The USGS defines a hydrograph as “a graph showing stage, flow, velocity, or other property of water with respect to time.” (Langbein and Iseri, 1960). Note there is no rigid requirement that a time axis be used when plotting time-base data, though this is the most common method. Another approach is demonstrated in this paper.

Lag-1 Hydrograph Method

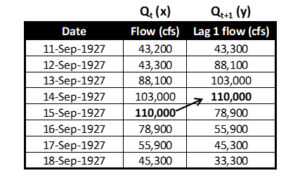
Data preparation and plotting are identical to an autocorrelation lag 1 plot, where 1 indicates a 1-day time shift. Table 1 shows how the time-series discharges are shifted. For this paper, the unshifted discharge is labeled Qt (the x coordinate) and the shifted discharge Qt+1 (the y coordinate). It is critical that the temporal sequence is maintained for the data. Thinking of the x values as “flow for today” and the y values as “flow for tomorrow” helps to visualize the order of the data.

 

Table 1. Data shift example (USGS site Colorado River at Lees Ferry, AZ)

To calculate discharge change, a ratio between the coordinates is used. This ratio can be used as a reference on the plot. For these equations below, the (x,y) coordinate is (Qt, Qt+1). In all cases there is a 1-day time step so that the change in time (Dt) is 1.

Equation 1a             y = mx  

Equation 1b             Qt+1 = m Qt

where m = change ratio

Equation 2              m = y/x = (Qt+1) / (Qt)                   

                               where m > 1, discharge is increasing

          m = 1, no change to discharge

                                         m < 1, discharge is decreasing

Equation 3a              y – x             = Qt+1 – Qt     = DQ/day    

Equation 3b              (m – 1) Qt   = Qt+1 – Qt = DQ/day

 

A traditional line hydrograph for the data in Table 1 is shown in Figure 1.

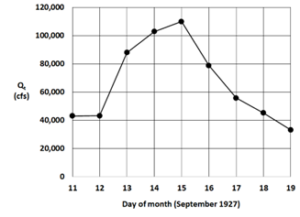
Figure 1. Line hydrograph for the Colorado River at Lees Ferry, AZ

 

The hydrograph represents runoff from a Pacific hurricane remnant that crossed into the southwestern United States (Weaver, 1968). The multiday event provides a useful example to display and discuss properties of the Lag-1 hydrograph.

A key item with this approach is that time is employed as a data attribute rather than as a coordinate. The lag-1 hydrograph (Figure 2) allows for additional information such as regions of increasing, decreasing or no change in discharge. An interesting feature of this plot is that the first and second order derivatives of the discharge are displayed.

Consider the following data representations on a Lag-1 hydrograph:

1.  The x coordinate of a data point represents the daily discharge (Qt)

2.  Each data point represents DQ/day or dQ/dt (1st order derivative)

3.  Lines connecting points represent D(DQ/day) or d2Q/dt2 (2nd order derivative)

The details listed above are comparable to distance (item 1), velocity (item 2), and acceleration (item 3) from the physics of motion. Regions are highlighted below.

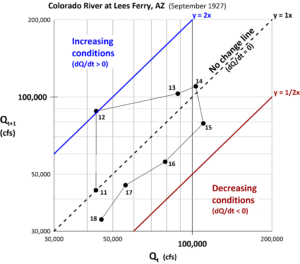
Figure 2. Lag-1 hydrograph example (day number associated with Qt).

 

Results

Figures 1 and 2 use the same data but display very different graphics.

Below are detailed comparisons of the two plots:

Days 11 to 12 – The line hydrograph shows little change between these two days, while the lag-1 hydrograph shows a single point very close to the y = 1x ratio change line.

Days 12 to 13 and 13 to 14 – The line hydrograph shows the rising limb of the event. The lag-1 hydrograph shows days 11, 12, 13, and 14 are all above the 1x line, indicating rising flow conditions. But because the distance of the points decreases from the 1x line, this shows the increases are occurring, but at a decreasing rate. Day 14 shows the peak for Qt+1, while Day 15 shows the peak for Qt. Both represent the discharge on 15 Sept 1927.

Days 15, 16, 17 and 18 – the line hydrograph shows decreasing flows. The lag-1 hydrograph also shows the decreasing flow conditions as all points are below the 1x line.

Additionally, the rate of change for the decrease is consistent. A power curve fitted to these points yields a recession equation for the general form aQb where Qt+1 = 1.8124 Qt 0.9198. This is consistent with the extraction method of baseflow recession segments based on a second-order derivative (Yang, et al., 2020).

 

Discussion & Conclusion

This paper is a brief overview of a new technique that does not appear elsewhere in the published literature. Here are three ways this technical approach can be used in water resources projects. First – use this method for model calibration by having the x axis be the observed data and the y axis be the modeled data. The resulting plot would be an “error hydrograph” showing time and discharge differences. Next – scale up the data used from one runoff event to a multi-year discharge record with the x axis as Qt and the y axis as Qt+1. The resulting plot becomes an autocorrelation lag 1 plot but now with the Q, dq/dt and d2Q/dt2 regions. Additionally, the autocorrelation r(k), a metric of persistence and randomness, can be calculated. Finally – let an upstream gaging station be the x axis and a downstream station, lagged by the routing time, be the y axis. The resulting plot will show the contribution of the local, ungaged area between the two stations.

A more in-depth treatment of this novel approach is available as a webinar (June 16, 2022) sponsored by the American Institute of Hydrology (AIH webinar, 2022).

Remarks

The author thanks AIH for the opportunity to share this self-funded research.

References

AIH webinar. 2022. A Novel Approach to Quantify Streamflow Properties, https://www.aihydrology.org/aih-webinar-a-novel-approach-to-quantify-streamflow-properties/

Langbein, W. B., and Iseri, Kathleen T., 1960. General Introduction and hydrologic definitions: U.S. Geol. Survey Water-Supply Paper 1541-A, 29 p.

Weaver, R. 1968. Meteorology of Major Storms in Western Colorado and Eastern Utah. Technical Memorandum WBTM HYDRO-7. U.S. Dept. of Commerce, Environmental Science Services Administration, Weather Bureau.

Yang, W., C. Xiao, and X. Liang. 2020. Extraction Method of Baseflow Recession Segments Based on Second-Order Derivative of Streamflow and Comparison with Four Conventional Methods. Water. 12. 10.3390/w12071953.

About the Author

Dr. Koehler is the CEO of Visual Data Analytics and a certified professional hydrologist with over 40-years’ experience.

Previously he was the National Hydrologic and Geospatial Sciences Training Coordinator for NOAA’s National Weather Service and is a retired NOAA Corps lieutenant commander. Assignments included navigation and operations officer for two NOAA oceanographic research ships, the Colorado Basin River Forecast Center and the Northwest River Forecast Center where he oversaw the implementation of an operational dynamic wave model for Lower Columbia River stage forecasts. Other positions include Director of Water Resources for an Arizona consulting company and the water resources hydrologist for Cochise County, Arizona. 

He is also a member of the science department faculty at Front Range Community College and is instructor for astronomy, geology, geography, GIS and geodesy courses. He is also an FAA certified professional drone operator.

He has a PhD, MS and BS in Watershed Management from the University of Arizona and an additional MS in Hydrographic Sciences from the US Naval Postgraduate School. The focus of his research are alternate methods of analyzing environmental time-series data along with associated data visualizations. 

Hydrologic Engineering Center Hydrologic Modeling Systems (HEC-HMS) version 4.10

By: HEC-HMS Team

Introduction

The Hydrologic Modeling System (HMS) is software developed by the Hydrologic Engineering Center designed to simulate precipitation-runoff processes of dendritic watershed systems. HEC-HMS provides a wide range of scalable methods for modeling hydrologic processes, delivers a modern and efficient user interface, supports robust optimization and uncertainty analysis capabilities, and has available complete documentation and training options for the engineering community. It is designed to be applicable for a wide range of geographic areas to solve the widest possible range of problems. This includes large river basin water supply and flood hydrology, and small urban or natural watershed runoff. 

The HEC-HMS team has recently modernized its software development process following Continuous Integration & Continuous Delivery principals. The results have been faster releases of new features, quicker turnaround for bug fixes, lower bug count in the official release, and easier collaboration with other developers. The current development version of HEC-HMS is version 4.10, which is planned to be released by summer of 2022. HEC-HMS version 4.10 includes numerous updates to the software, including a new compute option, new and refined meteorological methods, enhanced methods to display spatial results, and many more improvements. Other improvements and features that will be released with 4.10 include: 

  • Dynamic Reservoir Volume Reduction Method
  • Simplex Optimization Improvements
  • Resume Differential Evolution Optimization
  • Normalized Nash-Sutcliffe Efficiency Optimization Objective Function
  • Peak-Weighted Variable Power Optimization Objective Function
  • Snowmelt Plots
  • 2D Diffusion Wave Transform and 2D Sediment Transport Enhancements

We encourage users to visit the HEC-HMS webpage to learn more about current software updates: https://www.hec.usace.army.mil/confluence/hmsdocs/hmsum/latest/release-notes/v-4-10-0-release-notes

Frequency Analysis Compute

The new Frequency Analysis compute option in HEC-HMS is similar in nature to the existing Depth-Area Analysis framework that analyzes multiple points within a watershed at a single frequency. The Frequency Analysis compute option allows the user to analyze a single point over a range of different frequencies. A Frequency Analysis can have one to many ordinates defined, each with their own assigned annual exceedance probability, meteorological model, and basin model. Currently, the analysis can be used to generate a flow frequency curve or a stage frequency curve at the point of interest. Figure 1 shows the computed peak flow frequency curve output window from HEC_HMS at a specified location. 

Figure 1: Peak flow frequency curve generated from Frequency Analysis compute option

Interpolated Meteorology 

An interpolation option was added to the precipitation, temperature, windspeed, solar radiation, and evapotranspiration methods in the meteorological model. The interpolation option interpolates between gaged locations and creates a series of time-series grids over a gridded domain, or time-series at point locations if interpolating over a non-gridded domain. The interpolation can be performed over a range of time increments (daily, sub-daily, etc.) and simulation time-steps. The interpolation methods include inverse-distance squared, inverse-distance, nearest-neighbor, and bilinear. There is an option to bias correct a precipitation interpolation and lapse adjust a temperature interpolation. The interpolated results are cached to disk in an HEC-DSS file. The cached results are accessed on subsequent computes, unless a parameterization change occurs and invalidates the cache, triggering a re-compute. The time-series gages that are selected for interpolation must be parameterized with a valid longitude and latitude. Figure 2 shows the HEC-HMS Map Window demonstrating the interpolated precipitation capabilities for the Truckee River watershed.

Figure 2: Interpolated precipitation grid computed from point rainfall gages and PRISM bias grid using the Interpolated Precipitation meteorological method

Frequency Storm Meteorological Model Enhancements

New features for the Frequency Storm and Hypothetical Storm precipitation methods streamline their use for flow-frequency simulations. Multiple precipitation frequency grids downloaded from NOAA Atlas 14 can now be imported using the Precipitation Frequency Grid Importer. This feature also internalizes external source files for the grids by copying them to the project directory. The Frequency Precipitation Calculator tool can be used to quickly calculate average precipitation depths. These computed precipitation depths can be applied at either the watershed or subbasin level. Figure 3 shows the Frequency Precipitation Calculator. The Frequency Depths Calculator is only available if the meteorological model has been linked to a subbasin model that contains georeferenced subbasin elements. 

Figure 3: Frequency Precipitation Calculator using NOAA Atlas 14 Precipitation-Frequency grids

The frequency storm meteorological model also allows for a User-Specified area reduction method to be applied, shown in Figure 4. This new option allows the user to specify a depth area-reduction function and apply it to each of the inner durations of a frequency storm. 

Figure 4: User Specified Areal reduction factor for each precipitation duration

Viewing and Exporting Spatial Results

The HEC-HMS team is constantly developing new and improved options for visualizing model results. Evaluating model performance is critical for model refinement and conveying results. A legend, scale bar, and north arrow can now be displayed within the desktop when a valid spatial result or calibration metric is selected. These options can be enabled through the View menu. An example of these new visualization items is shown in Figure 5. Additionally, Min and Max buttons were added to the Spatial Results toolbar that allow for quick visualization of the minimum or maximum values of any spatial result regardless of the time in which they were computed. 

Figure 5: Legend, scale bar, and north arrow displayed for the Truckee River watershed Map window.  Min and Max buttons also shown on Spatial Results toolbar

An Export Snapshot button and an Export Recording button were added to the Spatial Results toolbar. The Export Snapshot button, when pressed, will allow the user to export the currently selected spatial result at the current display time step as a GeoTIFF file. The resultant file will be georeferenced and can be read by common GIS software (e.g., QGIS, ArcGIS). The Export Recording button, when pressed, will allow the user to export an animation of the currently selected spatial result to either AVI or MP4 file. The resultant animation will also include any currently displayed maps, such as subbasin outlines, reservoir icons, and terrain.

The Spatial Results toolbar can show calibration results for flow and snow water equivalent (SWE). This feature adds visuals for assessing the calibrated state of a basin model. Computed statistical metrics, such as Nash Sutcliffe Efficiency (NSE), Coefficient of Determination (R2), Root Mean Square Error / Standard Deviation (RSR), and Percent Bias (PBIAS), are used to color-code each subbasin, as shown in Figure 6. 

Figure 6: Spatial Results calibration results map layer for flow 

 

About Authors

The HEC-HMS Team consists of Matthew Fleming, Thomas Brauer, Michael Bartles, Gregory Karlovits, Jay Pak, Nick Van, Josh Willis, Daniel Black, Natasha Sokolovskaya, Alex Sanchez, Alex Davis, and David Ho. Team members all work for the U.S. Army Corps of Engineers and come from a wide variety of backgrounds – Civil Engineers, Hydrologists, Geologists, and Computer Scientists. All team members are competent in multiple disciplines of HMS teamwork, such as developing the software, testing the software, documenting, training, providing technical support, and supporting with hydrologic studies.

Any questions about this article can be directed to David Ho at David.ho@usace.army.mil

 

References

Gene Kim, Patrick Debois, John Willis, and Jez Humble. 2016. The DevOps Handbook: How to Create World-Class Agility, Reliability, and Security in Technology Organizations. IT Revolution Press.

Introduction to the GroundwaterU Video Public Library | July 13 Webinar

AWRA and AIH | Introduction to the GroundwaterU Video Public Library – a new and free educational resource.
Please join us for a special AIH webinar on  July 13, 2022 | 1:00 – 2:00 PM ET

DESCRIPTION
The GroundwaterU Video Library is a free, online catalogue of high-quality educational videos for all things groundwater – from science and engineering to law and policy, in multiple languages and from around the world. An educational platform that serves to make groundwater knowledge accessible globally by way of high-quality and engaging educational videos. This presentation will describe the goals and value of the GroundwaterU education initiative, how to use the website, and how volunteers can share their own expertise with a global audience via customized videos at no cost.

LEARNING OBJECTIVES
Advocate the use of the GroundwaterU Video Library to help facilitate the spreading of groundwater knowledge. Give attendees the knowledge about the need for global groundwater education. Prepare attendees with the necessary directions for using the online library.
WEBINAR RECORDING & PDH CERTIFICATE
Included with your webinar registration is access to a recording of the program and a fillable certificate to self-report your Professional Development Hour (PDH)/Continuing Education Credit (CEU). Your certificate will be available to download and a link to the recording of this webinar will be sent within a week of the live program from membership@awra.org. The recording is exclusively for you, the registrant of the webinar. They are not to be shared or forwarded.

Promo codes AIH members (and non-members) should use to register for the webinar are as follows:
AIHM22 – AIH Members to pay $0.00
AIHNON22 – AIH nonmembers to pay $25.00 (used for tracking purposes only as this is the same price as AWRA nonmembers)

Register Today

About The Speaker: Andrew Cohen is a hydrogeologist located in New Jersey, USA. He received a Ph.D. from the University of California at Berkeley. His focus is hydrogeologic investigations, contaminant fate and transport, conceptual site models, and groundwater education. Prior to his current roles in the environmental consulting industry and Adjunct Professor of Contaminant Hydrogeology at the New Jersey Institute of Technology, he was a Research Associate at Lawrence Berkeley National Laboratory, where he focused on hydrogeologic characterization and modeling of groundwater in fractured and faulted bedrock. He is now focused on the development of a free, online library of groundwater educational videos called the GroundwaterU Video Library, which he founded in January of this year.

President’s Message

AIHPresident Jamil Ibrahim

Greetings! The end of the calendar year is a common period for self-reflection by individuals and organizations. As I look back while concluding the first year of my two-year term as your American Institute of Hydrology (AIH) President, I’m delighted about the accomplishments of your AIH leadership team during 2021. Our achievements this year, however, are not just a function of what we did during 2021 – they consider the steps taken by AIH over the past few years to address challenges and introduce new perspectives, along with the great work of your leadership team.

We did great things in 2021! Thank you to all who contributed. Here’s a snapshot of our accomplishments:

  • Boosted AIH’s membership by 22% compared to 2020 and received 35% more new member applications during 2021 compared to the previous year.
  • Held the Institute’s first virtual meet-and-greet event with AIH members.
  • Connected our AIH community through in-person Water New Year celebrations in Minneapolis, Minnesota and Sacramento, California. One of the three co-founders of AIH, Roman Kanivetsky, joined in the Minneapolis event!
  • Welcomed our first Hydrologic Technician (HT) to serve as a member of AIH’s leadership team on our Executive Committee (EC).
  • Completed a widely popular and informative webinar series on the topic of Forecast Informed Reservoir Operations (FIRO). Our FIRO series, provided in collaboration with the American Water Resources Association (AWRA), featured our nation’s top experts on FIRO, an innovative strategy for water resources management that leverages use of advanced hydrological and meteorological data.
  • Convened a new Diversity, Equity, and Inclusion (DEI) Task Force composed of AIH members and members from the EC. Stay tuned – you will have an opportunity to learn more and support the important activities our DEI Task Force will be initiating within the next few months.
  • Revamped our membership application and database system. Despite the glitches our administration team encountered after the rollout, we’re confident our modernization changes will improve ease of application development by prospective members, application review and processing by our Board of Registration, and provide enhanced member benefits through access of information and content.
  • Presented to audiences at professional conferences about AIH and the importance of Professional Hydrologist (PH) certification for hydrologists and HT certification for hydrologic technicians, including: Groundwater Resources Association of California’s (GRAC) Future of Water Conference; Consortium of Universities for the Advancement of Hydrologic Science’s (CUAHSI) Biennial Colloquium; AWRA’s 2021 Annual conference; and the University of Minnesota’s 2021 Minnesota Water Resources Conference.
  • Improved social media presence and member connectivity.
  • Coordinated with researchers for the U.S. Department of Labor on development of information on hydrologist and hydrologic technician occupations.

Also, we are nearly complete with revisions and updates to AIH’s Bylaws and a contracting solicitation for AIH examination support services–both scheduled for distribution early in 2022.

Again – Thank you to all who have stepped forward to take on roles to help advance the mission of AIH. Member participation is vital to AIH’s success and we are eager to engage more members in AIH activities. Even if not interested in taking on a leadership role for AIH or getting involved in various subcommittees or groups, we request all our members to be ambassadors for AIH and its certified members. Please contact me or others on our leadership team to learn more about how to get involved.

Sincerely,

Jamil S. Ibrahim PH, PMP, ENV SP

AIH President, 2021-2022

Former AIH President Delivers a Keynote Address at the Latin American Congress of Civil Engineering Students

Former AIH President Delivers a Keynote Address at the Latin American Congress of Civil Engineering Students

From November 14-20, 2021, over 120 civil engineering students from nine Latin American countries attended the COLEIC (Latin American Congress of Civil Engineering Students) 2021 event in Tarija, Bolivia.

Dr. Miguel A. Medina, Jr., PH (AIH President, 2009-2010) delivered a keynote presentation on November 17th titled “Water Resources of Bolivia, Integration of Hydrologic Cycle Processes, Climate Change Challenges, Adaptation and Professional Opportunities.” That same day he was invited to the Municipality of Tarija and presented with an ordinance declaring him a Distinguished Visitor. While at the Tarija City Hall, he was interviewed by a local journalist regarding his findings of potential climate change in Tarija.

Medina

The following morning a national Bolivian TV (UNITEL) news crew interviewed him live at the Hotel Vendimia lobby on the topic of Bolivian water resources and management, as well as potential climate change implications. The broadcast was also presented again that evening on a national news segment.

On November 18th, Medina also participated in a forum discussion on climate change implications for the civil engineering and hydrology professions.

For his presentation, Medina examined the annual maxima series of precipitation at three recording stations in the region: Tarija (1944-2020), Juntas (11976-2020) and Cañas (1977-2020).

Nonstationary time series analysis with the Generalized Extreme Value Distribution (GEV) was applied to the three stations.

Both Tarija and Juntas exhibited a slight decrease in precipitation. However, at a higher elevation over a mountain ridge, Cañas exhibited a substantial increase in precipitation.

Both deterministic and statistical methods were discussed, as well as surface-subsurface interactions across the hydrologic cycle. The presentation ended with recommendations for infrastructure adaptation to climate change, increased monitoring needs, and a review of current standards. Specific recommendations followed for future training of civil engineers and hydrologists to enhance their professional opportunities.

Institute Development Recap

Institute Development Recap

This past fall, the American Institute of Hydrology participated in two hydrology related conferences: 2021 Minnesota Water Resources Conference (MWRC) on October 19, 2021 and the American Water Resources Association (AWRA) on November 10, 2021.

Minnesota Water Resources Conference
Minnesota Water Resources Conference

At the MWRC conference, Salam Murtada (VP of Institute Development), Brennon Schaefer (VP of Communication) and John Nieber (past president of AIH) co-authored a presentation titled “American Institute of Hydrology: Certifying the Practice of Hydrology”. The presentation provided an overview of AIH, history, current membership composition, certification process and on-going activities. It was attended by over 100 people. The conference, which was held virtually this year, was attended by over 800 water resources professionals representing students, university teachers, consultants and government officials at the federal, state and local levels. The MWRC is held annually around the middle of October in St. Paul, Minnesota.

At the AWRA conference, AIH participated at the gold level sponsorship. During the reception, Salam Murtada gave a brief presentation about AIH followed by award announcements for three outstanding hydrologists: Vicki Kretsinger Grabert who was awarded the Charles V. Theis Award for contributions to groundwater, Dr. Phil Bedient who was awarded the Ray K. Linsley award for contributions to surface water and Dr. Ying Ouyang who was awarded the Robert G. Wetzel award for contributions to water quality. The AWRA conference was also held virtually this year due to the pandemic.

Vicki Kretsinger Grabert, PH     Dr. Phil BedientDr. Ying Ouyang, PH
Charles V. Theis Award for Contributions to GroundwaterRay K. Linsley Award for Contributions to Surface WaterRobert G. Wetzel Award for Contributions to Water Quality

We hope to continue collaborating with MWRC, AWRA and other organizations such as the Consortium of Universities for the Advancement of Hydrologic Science, Inc (CUAHSI), Groundwater Resources Association (GRA) and the American Geoscience Institute (AGI) among many others.