By Theodore .V. Hromadka II (1) and Prasada Rao (2)
(1) Professor, Department of Engineering-Mathematics, United States Military Academy, West Point, NY.
(2) Professor, Department of Civil and Environmental Engineering, California State University, Fullerton, CA.
Abstract
For simulating flows where inertial forces dominate over frictional forces, as in many types of floods, the solution of the two dimensional diffusion wave equation will suffice (compared to a one dimensional simulation). The associated numerical models are reliable and computationally efficient, thus not warranting the amount of resources that are required for solving the full momentum equations. In this work, the reliability of the USGS Diffusion Hydrodynamic Model (DHM) is cross checked by comparing its results with the more widely used HEC-RAS model. The close agreement between the two sets of computational results underscores the reliability of the legacy DHM.
Key words: Two dimensional models, Diffusive wave, HEC-RAS, DHM
Introduction
Numerical models developed in the 1980’s and earlier, during which period, computer memory and speed were significant modeling constraints, are increasingly called “legacy” models. The mathematical underpinnings in these models coupled with their reliability has made their solution to serve as a benchmark solution for the modern software. That is, providing another computational opinion to the problem under study using the prior technology. While some legacy models have been altered to accommodate more complex fluid dynamics (by adding modules to simulate flow turbulence, simplifying the data input requirements, and/or enhancing the model output/visualization modules), other legacy models have focused on access to their core algorithms, laying a foundation to newer models. DHM [1] is an example of such a legacy, first generation, hydraulics model developed for the USGS in the mid 1980’s time period, which led to publication of a USGS Technical Report in 1987. The model was written in Fortran 77, and has been extensively applied to different overland, coupled channel, and overbank flow scenarios. The DHM also served as a foundation for other finite-difference algorithms [2] resulting in additional computational programs for solving a variety of transport problems.
DHM solves the two-dimensional overland flow equations coupled with one-dimensional open channel flow equations and includes interfaces between these two flow regimes using source and sink term approximations. It is one of the first general purpose computational solutions to a two dimensional formulation of the Navier-Stokes equations. The model is capable of approximating such hydraulic effects as backwater, drawdown, channel overflow, storage, and ponding, among other hydraulic topics of interest.
The application of legacy hydraulic models, including DHM, for large-scale applications on modern computers is constrained by multiple factors. One is related to recompiling the code to take into account new processors and architecture. Porting the Fortran 77 codes to the new computing platforms and recompiling them can be a challenge and may warrant rewriting some coding statements that are not supported by the new compilers. Changes to the legacy codes may require adding new functionalities. In this case, the DHM code was re-compiled using the Intel visual Fortran compiler. The end windows environment executable file is robust, and the time required to run the model, because of the various optimization modules in the compiler, has been significantly reduced. Another factor is that DHM was written when memory requirements in computers were limited. This limitation translated to using a smaller size of the arrays, and hence its application over large-scale computational domains was not feasible. To address this, the legacy codes can be modified to include the array standards that were introduced to Fortran in the 2000’s timeframe. The size of the dimension array in the DHM was increased from 250 to 9999. Larger arrays are possible as well. Similarly, for codes in which the system of equations is assembled into the matrix form Ax=B, the solver phase can incur a large cost. Matrices are often so large that the standard numerical methods become unsatisfactory and cannot be implemented on even high-performance computers. In a typical code, the largest portion of CPU time is spent in solving systems of linear algebraic equations [4]. It is noted that for an applied researcher, a solution module merely represents a means to an end of solving the flow equations, while for a “solver” developer, the application is a source of sparse equations to be solved. In such cases, using an appropriate solver coupled with a pre-conditioner can make the legacy codes more computationally efficient.
In this work, the results from DHM are compared with those of HEC-RAS (ver. 5.07) for a flow scenario accompanied by a flood. Our primary goal is to underscore the reliability of DHM.
Overview of the Models
DHM was developed for the USGS in the late 1970’s and is one of the first computational hydraulics programs. It solves the simplified Navier-Stokes equations written in diffusion form. For the uniform grid elements, the integrated finite difference version of the nodal domain integration method is used for solving the equations. Characteristic features of the DHM include (a) computational domain is made of square cells; (b) flow can enter or leave the cell through any of the four interfaces (c) minimum and maximum time step size that can be used in the computation needs to be specified, and (d) flow variables are calculated at the center of the cell. The required input conditions at the center of each cell are bottom elevation, initial water depth, and roughness value; The model uses an integrated finite difference numeric scheme for solving the flow equations. The model’s companion website www.diffusionhydrodynamicmodel.com has the relevant source codes, executable files, and complete documentation along with the results from various case studies of applications.
HEC-RAS allows the user to perform one-dimensional steady flow, one and two-dimensional unsteady flow calculations, sediment transport, and water quality modeling [4]. It gives the option of either solving the two dimensional diffusion wave (default mode) or the full dynamic equations. HEC-RAS and DHM share many similarities in that both models calculate the flow variables at the center of the computational cell with the given input details at the center of the cell (elevation, roughness value, initial depth). HEC-RAS uses an implicit finite volume solution of the flow equations. The model provides the flexibility of generating either uniform square, hexagonal, or adaptive mesh, based on the terrain characteristics. It also offers many other features for solving one and two dimensional steady and unsteady river flow simulations like coupling one and two dimensional models, computational mesh development and refinement tools, geometric and hydraulic input and output tools, multiple boundary options, moving sediment and water quality analysis tools, and other options as discussed in the current version of the HEC-RAS user manual [4].
Case Study Test Problem and Flow Details
In the case under study, a rectangular channel is specified that is 41 miles long and 800ft wide with a longitudinal slope of 2.48%. The computational domain is discretized using uniform square cells of dimensions 160ft x 160ft. There are a total of 9471 cells defined in the test model domain. The two channel “walls” defined by the DHM were modeled by cells with high bottom elevations. The simulation was performed over 73 hours. An initial water depth of 0ft in all the cells was specified. The inflow hydrograph (Figure 1) was specified at the center cell of the upstream end. The inflow has a peak value of 79141 cfs at time = 36 hours and a flow of 16500 cfs at time = 72 hours. A critical depth boundary condition was specified along the downstream boundary nodes. Of interest is the cumulative outflow at the downstream boundary.
Computational Results
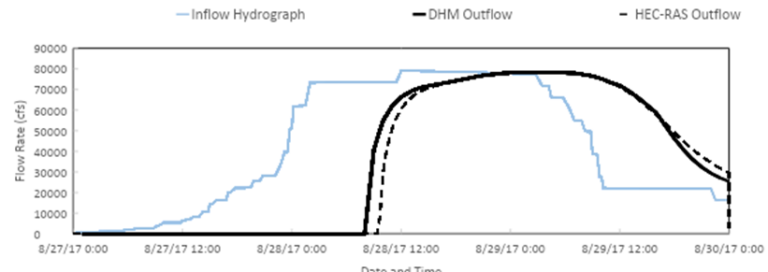
Figure 1 plots the inflow hydrograph and the two outflow hydrographs for a channel bottom Mannings roughness (n) value of 0.035. The peak outflow and its time of arrival, which are of primary interest in the analysis, are similar for both the configured models. The program’s default values (like tolerance variables, time step, threshold values, etc.) were used, and no effort was made to optimize them.
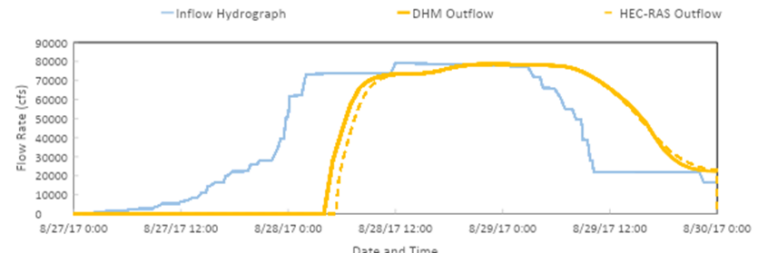
Figure 2 plots the corresponding outflow hydrographs for a channel bottom roughness (n) value of 0.06.
The demonstration problems show that the considered two computational models can produce very similar outcomes. This is an important result because the two models differ in their underpinnings. The respective partial differential equations being modeled differ, and the computational efforts also differ, causing a difference between the two modeling outcomes. However, the computational effort needed to use the HEC-RAS model is substantially more than the DHM formulation, which calls into question the use of the HEC-RAS in similar practical problems. It is noted that a recent advance in the DHM is a code that runs on a hand-held calculator.
Conclusions
In this effort, the performance characteristics of two well-known hydraulic models, HEC-RAS and DHM are analyzed. The focus was on comparing their respective solution of the two dimensional diffusion flow equation. Given that the Diffusive Wave formulation of the flow equations is the HEC-RAS default option, and the Diffusive Wave formulation is also the default flow routing option in the legacy program DHM, a unique opportunity exists to test both computational programs and compare outcomes. The reliability of DHM, being one of the first computational models for solving the simplified overland flow equations, was reinforced by comparing its output with the HEC-RAS output. It is concluded that other computational outcomes from legacy models like DHM can act as a baseline analysis for new computational models and paradigms that continue to evolve.
Author Details
Hromadka & Associates’ Principal and Founder, Theodore Hromadka II, Ph.D., Ph.D., Ph.D., PH, PE, has extensive scientific, engineering, expert witness, and litigation support experience. His frequently referenced scientific contributions to the hydrologic, earth, and atmospheric sciences have been widely published in peer-reviewed scientific literature, including 30 books and more than 500 scientific papers, book chapters, and government reports. His professional engineering experience includes supervision and development of over 1500 engineering studies. He is currently a faculty member at the United States Military Academy at West Point, New York.
Prasada Rao is a Professor in the Civil and Environmental Engineering Department at California State University, Fullerton.
References
1. Hromadka II TV, Yen CC. A diffusion hydrodynamic model. Water resources investigations report. U.S. geological survey; 1987: 87– 4137, https://pubs.er.usgs.gov/publication/wri874137
2. O’Brien JS, Julien PY, Fullerton WT. Two‐dimensional water flood and mudflow simulation. J Hydraulic Eng ASCE. 1993; 119: 244–261.
3. Eriksson K, Estep D, Hansbo P, and Johnson C. Computational Differential Equations. Cambridge University Press, New York, 1996.
4. Brunner, GW., CEIWR-HEC, US Army Corps of Engineers, HEC-RAS River Analysis System, 2D Modeling User’s Manual, Version 5.07, March 2021. https://www.hec.usace.army.mil/software/hec-ras/
