An Improvement to the Node Positioning Algorithms of the Method of Fundamental Solutions and Complex Variable Boundary Element Method
Authors:
Sebastian A. Neumann1, Saleem A. Ali2, Theodore V. Hromadka II3
1Cadet, United States Military Academy, United States of America
2Cadet, United States Military Academy, United States of America
3Distinguished Professor, United States Military Academy, United States of America
1 Abstract
In this work we examine use of various geometries and schemes for defining computational node positions on the complex plane. Circular patterns may be of interest for problems involving groundwater well fields or studies of well placement spacing and the like. This contrasts with existing methods, which used candidate nodes and refined them based on performance. One of the most pertinent use-cases we discussed when working on this method was the case of pinpointing the source water contamination in a suburban/urban setting. With existing methods, it is challenging to accurately model the flow of drinking water as it moves from supplier to consumer. This can become an issue if it gets contaminated at some point along the pipe. With some refinement, we believe this new method can be used to efficiently model fluid flow through potable water pipes, allowing investigators to generate a more accurate picture of possible contamination sources, allowing for better resolution of the crisis.
2 Literature Review
The Complex Variable Boundary Element Method (CVBEM) was used for modeling groundwater transmission by Wilkins et al.,[1]. The Wilkins method generates an initial distribution of node candidates, and gradually introduces these candidates into the final model, optimizing for the lowest error on the boundary. Also of note is the work of DeMoes et al.,[2], who detail in their paper the method iterated upon by Wilkins et al.
3 Methods
The CVBEM method for solving 2-dimensional boundary value problems positions a set of candidate nodes in a grad pattern outside the Study Domain. As more collocation points are added to the approximation function, nodes are chosen from this set and refined to give the best possible approximation for each given node (best being minimum difference between the known boundary function and the approximation function). In this work, we replace the existing method for positioning nodes with a less accurate, but more computationally efficient method.
In this method, rather than selecting candidate nodes and refining them, we simply generate the nodes based on a pre-determined probability density function. For our examples, we used a circle as the basic shape, then added variance to each point’s distance from the boundary (according to the normal distribution). This led to a band of points with some closer to the Study Domain and some farther away.
Now, rather than going through the much-laborious process of refining each candidate node each iteration of the algorithm (computationally, O(n2) time), we simply generate a pseudo-random point in accordance with the predefined probability distribution, which still proves to be quite effective and has a computational time of O(n).
4 Results
Overall, this method decreases accuracy by a factor of 102 while speeding up computation by a factor of 104. The charts below show a comparison between the two methods on some of the benchmark problems shown in the original CVBEM paper. Figure 1 shows a plot of the log of the error as the number of points is increased for our first benchmark – the 90-degree bend. Figure 2 shows the same plot but for our second benchmark – the 90-degree bend with a hump.
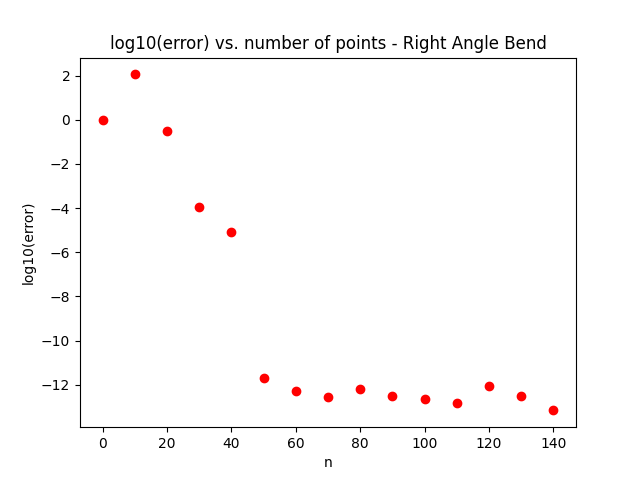
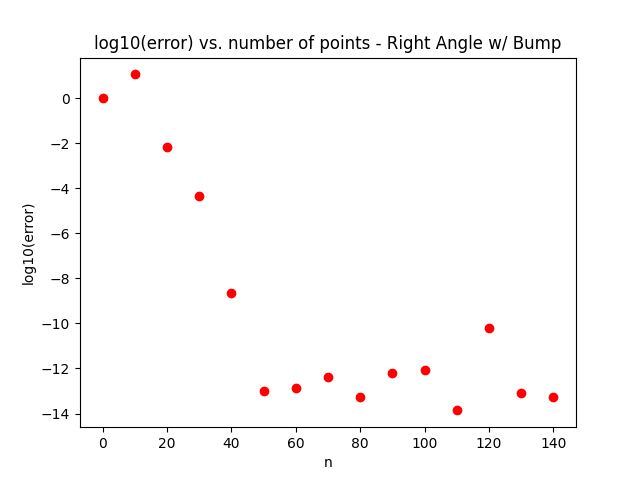
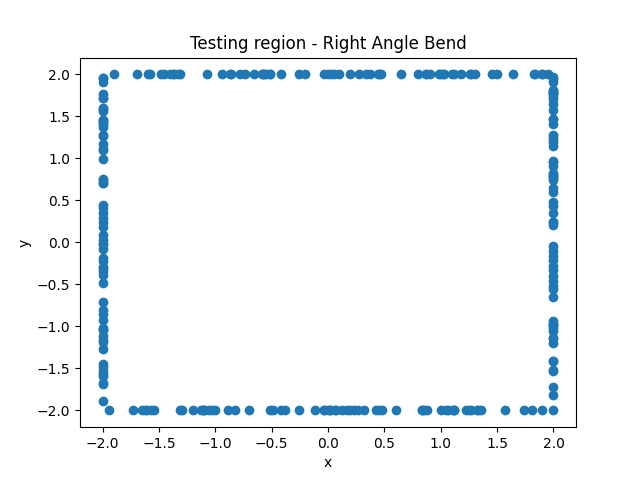
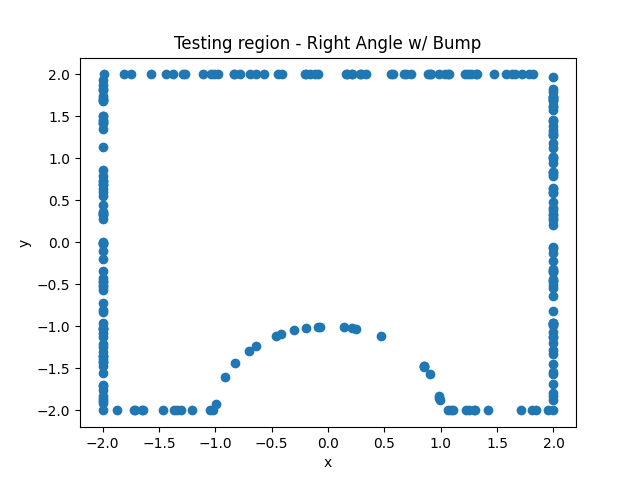
We noticed that the irregularity of the surface negatively contributes to the accuracy of the model. In Figures 3 and 4, we demonstrate the use of 150 node and collocation point pairs to generate our results and, in these specific problems, these were sufficient in lowering the maximum error to under 10−14. However, in the problem only concerning the 90-degree bend, this method was able to progress to a further 10−16, a significant improvement.
5 Conclusions
With the initial methods, we attempted to define a pure algorithm which has a basis in logic and mathematical principles. While this algorithm was effective, and could be shown to converge, it was impractical to implement for real-world simulations. The real world is messy, and the margin for error of measurements taken is far higher than any of our models introduce. For that reason, even though this new method loses some fidelity, this error is vastly outweighed by the errors created by measurement devices. By creating a faster, less computationally demanding algorithm, we can make it easier to implement in real-world applications.
6 Post-Script
Sebastian Neumann is a cadet at the United States Military Academy studying mathematics and computer science. In his free time, he enjoys tutoring his friends in various computer science classes and is working on an introductory video for all prospective CS majors at West Point.
References
[1] B. D. Wilkins, T. V. H. II, W. Nevils, B. Siegel, and P. Yonzon, “Using a node positioning algorithm to improve models of groundwater flow based on meshless methods,” 2014.
[2] N. J. DeMoes, “Optimization algorithm to locate nodal points for the method of fundamental solutions,” 2014.
